Most control systems utilize feedback in some manner. Here's a look at several fundamental feedback mechanisms, culminating in a description of a basic PID controller.
Many real-time embedded systems make control decisions. These decisions are usually made by software and based on feedback from the hardware under its control (termed the "plant"). Such feedback commonly takes the form of an analog sensor that can be read via an A/D converter. A sample from the sensor may represent position, voltage, temperature, or any other appropriate parameter. Each sample provides the software with additional information upon which to base its control decisions.
Closed-Loop Control
Systems that utilize feedback are called closed-loop control systems. The feedback is used to make decisions about changes to the control signal that drives the plant. By contrast, an open-loop control system doesn't have or doesn't use feedback.
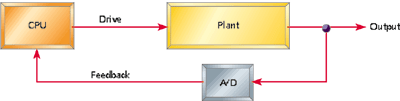
Figure 1. A closed-loop control system
A basic closed-loop control system is shown in Figure 1. This figure can describe a variety of control systems, including those driving elevators, thermostats, and cruise control.
Closed-loop control systems typically operate at a fixed frequency. The frequency of changes to the drive signal is usually the same as the sampling rate, and certainly not any faster. After reading each new sample from the sensor, the software reacts to the plant's changed state by recalculating and adjusting the drive signal. The plant responds to this change, another sample is taken, and the cycle repeats. Eventually, the plant should reach the desired state and the software will cease making changes.
If feedback indicates that the temperature in your home is below your desired setpoint, the thermostat will turn the heater on until the room is at least that temperature. Similarly, if your car is going too quickly, the cruise control system can temporarily reduce the amount of fuel fed to the engine.
Proportional Control
How much should the software increase or decrease the drive signal? One option is to just set the drive signal to its minimum value when you want the plant to decrease its activity and to its maximum value when you want the plant to increase its activity. This strategy is called on-off control, and it is how many thermostats work.
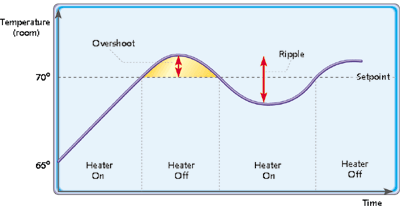
Figure 2. An example of on-off control
On-off control doesn't work well in all systems. If the thermostat waits until the desired temperature is achieved to turn off the heater, the temperature may overshoot. See Figure 2. The same amount of overshoot and ripple probably isn't acceptable in an elevator.
Proportional control is the primary alternative to on-off control. If the difference between the current plant output and its desired value (the current error) is large, the software should probably change the drive signal a lot. If the error is small, it should change it only a little. In other words, we always want a change like:
P * (desired - current)
where P is a constant proportional gain set by the system's designer.
For example, if the drive signal uses PWM, it can take any value between 0% and 100% duty cycle. If the signal on the drive is 20% duty cycle and the error remaining at the output is small, we may just need to tweak it to 18% or 19% to achieve the desired output at the plant.
If the proportional gain is well chosen, the time the plant takes to reach a new setpoint will be as short as possible, with overshoot (or undershoot) and oscillation minimized.
Unfortunately, proportional control alone is not sufficient in all control applications. One or more of the requirements for response time, overshoot, and oscillation may be impossible to fulfill at any proportional gain setting.
Derivative Control
The biggest problem with proportional control alone is that you want to reach new desired outputs quickly and avoid overshoot and minimize ripple once you get there. Responding quickly suggests a high proportional gain; minimizing overshoot and oscillation suggests a small proportional gain. Achieving both at the same time may not be possible in all systems.
Fortunately, we do generally have (or can derive) information about the rate of change of the plant's output. If the output is changing rapidly, overshoot or undershoot may lie ahead. In that case, we can reduce the size of the change suggested by the proportional controller.
The rate of change of a signal is also known as its derivative. The derivative at the current time is simply the change in value from the previous sample to the current one. This implies that we should subtract a change of:
D * (current - previous)
where D is a constant derivative gain. The only other thing we need to do is to save the previous sample in memory.
In practice, proportional-derivative (PD) controllers work well. The net effect is a slower response time with far less overshoot and ripple than a proportional controller alone.
Adding Integration
A remaining problem is that PD control alone will not always settle exactly to the desired output. In fact, depending on the proportional gain, it's altogether possible that a PD controller will ultimately settle to an output value that is far from that desired.
The problem occurs if each individual error remains below the threshold for action by the proportional term. (Say the error is 3, P = 1/8, and integer math is used.) The derivative term won't help anything unless the output is changing. Something else needs to drive the plant toward the setpoint. That something is an integral term.
An integral is a sum over time, in this case the sum of all past errors in the plant output:
Even though the integral gain factor, I, is typically small, a persistent error will eventually cause the sum to grow large and the integral term to force a change in the drive signal. In practice, the accumulated error is usually capped at some maximum and minimum values.
In summary, on-off and proportional control are the two basic techniques of closed-loop control. However, derivative and/or integral terms are sometimes added to porportional controllers to improve qualitative properties of a particular plant's response. When all three terms are used together, the acronym used to describe the controller is PID.
This article was published in the August 2002 issue of Embedded Systems Programming. If you wish to cite the article in your own work, you may find the following MLA-style information helpful:
Barr, Michael. "Closed-Loop Control," Embedded Systems Programming, August 2002 , pp. 55-56.
Related Barr Group Courses:
Embedded Linux Customization and Driver Development
For a full list of Barr Group courses, go to our Course Catalog.
