Whenever you connect two or more computers together with the intent of exchanging information, you assume that the exchange will take place without errors. But what if some of the data is lost or corrupted in transit? Communication protocols usually attempt to detect such errors automatically. To do that they use checksums.
Download Barr Group's Free CRC Code in C now.
The most important part of listening to someone speak is ensuring that you've heard them correctly. Your brain performs the tasks of error detection and correction for you, automatically. It does this by examining extra bits of information from the speaker and the speech; if a phrase or sentence makes sense as a whole and it makes sense coming from the mouth of the particular speaker, then the individual words were probably heard correctly. The same principle applies when you are reading. But what happens when computers are communicating with one another? How does the receiving computer know if an error has occurred in transmission?
Establishing correctness is more difficult for computers than humans. At the lowest level, communication between computers consists of nothing but a stream of binary digits. Meaning is only assigned to that particular sequence of bits at higher levels. We call that meaningful sequence of bits the message; it is analogous to a spoken or written phrase. If one or more bits within the message are inverted (a logic one becomes a logic zero, or vice versa) as it travels between computers, the receiver has no way to detect the error. No environmental or syntactical context is available to the receiver, since it cannot understand the message in its transmitted form.
Parity Bits
If we want communicating computers to detect and correct transmission errors automatically, we must provide a replacement for context. This usually takes the form of an error correction code or error detection code. A simple type of error detection code that you are probably already familiar with is called a parity bit. A parity bit is a single, extra binary digit that is appended to the message by the sender and transmitted along with it. Depending on the type of parity used, the parity bit ensures that the total number of logic ones sent is even (even parity) or odd (odd parity). For an example of even parity, consider the sequence:
10101110 1
in which the eight-bit message contains five ones and three zeros. The parity bit is one in this case to force the total number of ones in the transmitted data stream to be even.
When a parity bit is appended to a message, one additional bit of data must be sent between the computers. So there must be some benefit associated with the lost bandwidth. The most obvious benefit is that if any single bit in the message is inverted during transmission, the number of ones will either increase or decrease by one, thus making the received number of ones odd and the parity incorrect. The receiver can now detect such an error automatically and request a retransmission of the entire stream of bits. Interestingly, the receiver can also now detect any odd number of bit inversions. (Note that all of this still applies even when the parity bit is one of the inverted bits.)
However, as you may have already noticed, if two bits are inverted (two ones become zeros, for example), the parity of the stream of bits will not change; a receiver will not be able to detect such errors. In fact, the same is true for any even number of bit inversions. A parity bit is a weak form of error detection code. It has a small cost (one bit per message), but it is unable to detect many types of possible errors. (By the way, odd parity has the same costs, benefits, and weaknesses as even parity.)
Perhaps this is not acceptable for your application. An alternative that might occur to you is to send the entire message twice. If you're already spending bandwidth sending an error detection code, why not spend half of the bandwidth? The problem is that you could actually be spending much more than half of the available bandwidth. If a computer receives two copies of a message and the bits that comprise them aren't exactly the same, it cannot tell which one of the two is correct. In fact, it may be that both copies contain errors. So the receiver must request a retransmission whenever there is a discrepancy between the message and the copy sent as an error detection code.
With that in mind, let's compare the bandwidth costs of using a parity bit vs. resending the entire message. We'll assume that all messages are 1,000-bits long and that the communications channel has a bit error rate (average number of inverted bits) of one per 10,000 bits sent. Using a parity bit, we'd spend 0.1% of our bandwidth sending the error detection code (one bit of error protection for 1,000 bits of message) and have to retransmit one out of every 10 messages due to errors. If we send two complete copies of each message instead, the smallest unit of transmission is 2,000 bits (50% of our bandwidth is now spent sending the error detection code). In addition, we'll have to retransmit one out of every five messages. Therefore, the achievable bandwidths are approximately 90% and 40%, respectively. As the width of the code increases, the message plus code lengthens and becomes more vulnerable to bit errors and, as a result, expensive retransmissions.
From this type of analysis it should be clear that keeping the size of an error detection code as small as possible is a good thing, even if it does mean that some types of errors will be undetectable. (Note that even sending two copies of the message is not a perfect solution. If the same bit errors should happen to occur in both copies, the errors will not be detected by the receiver.) In addition to reducing the bandwidth cost of transmitting the error detection code itself, this also increases the message throughput. But we still don't want to go so far as using a one-bit error detection scheme like parity. That would let too many possible errors escape detection.
In practice, of course, we can achieve far better error detection capabilities than just odd numbers of inverted bits. But in order to do so we have to use error detection codes that are more complex than simple parity, and also contain more bits. I'll spend the remainder of this column and most of the next two discussing the strengths and weaknesses of various types of checksums, showing you how to compute them, and explaining how each can be best employed for purposes of error detection.
Checksums
As the name implies, a checksum usually involves a summation of one sort or another. For example, one of the most common checksum algorithms involves treating the message like a sequence of bytes and summing them. Listing 1 shows how this simple algorithm might be implemented in C.
uint8_t
Sum(uint8_t const message[], int nBytes)
{
uint8_t sum = 0;
while (nBytes-- > 0)
{
sum += *(message++);
}
return (sum);
} /* Sum() */
Listing 1. A sum-of-bytes checksum
The sum-of-bytes algorithm is straightforward to compute. However, understanding its strengths and weaknesses as a checksum is more difficult. What types of errors does it detect? What errors is it unable to detect? These are important factors to consider whenever you are selecting a checksum algorithm for a particular application. You want the algorithm you choose to be well matched to the types of errors you expect to occur in your transmission environment. For example, a parity bit would be a poor choice for a checksum if bit errors will frequently occur in pairs.
A noteworthy weakness of the sum-of-bytes algorithm is that no error will be detected if the entire message and data are somehow received as a string of all zeros. (A message of all zeros is a possibility, and the sum of a large block of zeros is still zero.) The simplest way to overcome this weakness is to add a final step to the checksum algorithm: invert the bits of the final sum. The new proper checksum for a message of all zeros would be FFh. That way, if the message and checksum are both all zeros, the receiver will know that something's gone terribly wrong. A modified version of the checksum implementation is shown in Listing 2.
uint8_t
SumAndInvert(uint8_t const message[], int nBytes)
{
uint8_t sum = 0;
while (nBytes-- > 0)
{
sum += *(message++);
}
return (~sum);
} /* SumAndInvert() */
Listing 2. A slightly more robust sum-of-bytes checksum algorithm
This final inversion does not affect any of the other error detection capabilities of this checksum, so let's go back to discussing the basic sum-of-bytes algorithm in Listing 1. First, it should be obvious that any single bit inversion in the message or checksum will be detectable. Such an error will always affect at least one bit within the checksum. (It could affect more, of course, but not less.) Observe that the sum-of-bytes is performed by essentially lining up all of the bytes that comprise the message and performing addition on them, like this:
10110101 11000000 00001101 + 11100011 ---------- 01100101
Because of this mathematical arrangement, simultaneous single-bit inversions could occur in each of any number of the "columns." At least one bit of the checksum will always be affected. No matter how the inversions occur, at least the lowest-order column with an error will alter the checksum. This is an important point, because it helps us to understand the broader class of errors that can be detected by this type of checksum. I'll say it again: no matter how the inversions occur, at least the lowest order column with an error will alter the checksum, which means that two or more bit inversions in higher-order columns may cancel each other out. As long as the lowest-order column with an error has only one, it doesn't matter what other errors may be hidden within the message.
Now let's step back for a minute and talk about errors more formally. What exactly does a transmission error look like? Well, the first and most obvious type of error is a single bit that is inverted. That happens sometimes and is easy to detect (even a parity bit will do the job). Other times, bit inversions are part of an error burst. Not all of the bits within an error burst must be inverted. The defining characteristic is simply an inverted bit on each end. So an error burst may be 200 bits long, but contain just two inverted bits--one at each end.
A sum-of-bytes checksum will detect the vast majority of error bursts, no matter what their length. However, describing exactly which ones is generally difficult. Only one class of error bursts is always detectable: those of length eight bits or less. As long as the two inverted bits that bound the error burst have no more than six bits between them, the error will always be detected by this algorithm. That's because our previous requirement for error detection--that the lowest-order column with an error have only one error--is always met when the length of the error burst is no longer than the width of the checksum. We can know with certainty that such errors will always be detected.
Of course, many longer error bursts will also be detected. The probability of detecting a random error burst longer than eight bits is 99.6%. Errors will only be overlooked if the modified message has exactly the same sum as the original one, for which there is a 2-8 chance. That's much better error detection than a simple parity bit, and for not too much more cost.
The sum-of-bytes algorithm becomes even more powerful when the width of the checksum is increased. In other words, increasing the number of bits in the checksum causes it to detect even more types of errors. A 16-bit sum-of-words checksum will detect all single bit errors and all error bursts of length 16 bits or fewer. It will also detect 99.998% of longer error bursts. A 32-bit sum will detect even more errors. In practice, this increase in performance must be weighed against the increased cost of sending the extra checksum bits as part of every exchange of data.
The Internet Checksum
Many protocol stacks include some sort of a checksum within each protocol layer. The TCP/IP suite of protocols is no exception in this regard. In addition to a checksum at the lowest layer (within Ethernet packets, for example), checksums also exist within each IP, UDP, and TCP header. Figure 1 shows what some of these headers look like in the case of some data sent via UDP/IP. Here the fields of the IP header are summed to generate the 16-bit IP checksum and the data, fields of the UDP header, and certain fields of the IP header are summed to generate the 16-bit UDP checksum.
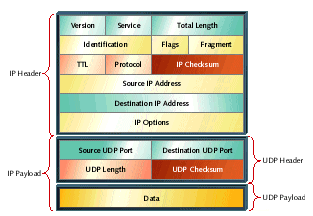
Figure 1. UDP and IP headers with checksum fields highlighted
A function that calculates the IP header checksum is shown in Listing 3. This function can be used before sending an IP packet or immediately after receiving one. If the packet is about to be sent, the checksum field should be set to zero before calculating the checksum and filled with the returned value afterward. If the packet has just been received, the checksum routine is expected to return a value of 0xFFFF to indicate that the IP header was received correctly. This result is a property of the type of addition used to compute the IP checksum.
uint16_t
NetIpChecksum(uint16_t const ipHeader[], int nWords)
{
uint32_t sum = 0;
/*
* IP headers always contain an even number of bytes.
*/
while (nWords-- > 0)
{
sum += *(ipHeader++);
}
/*
* Use carries to compute 1's complement sum.
*/
sum = (sum >> 16) + (sum & 0xFFFF);
sum += sum >> 16;
/*
* Return the inverted 16-bit result.
*/
return ((unsigned short) ~sum);
} /* NetIpChecksum() */
Listing 3. IP header checksum calculation
The IP header to be checksummed should be passed to NetIpChecksum() as an array of 16-bit words. Since the length of an IP header is always a multiple of four bytes, it is sufficient to provide the header length as a number of 16-bit words. The checksum is then computed by the function and returned to the caller for insertion into the header for validation of the header contents.
When you first look at this function, you may be overcome with a feeling of deja vu. The IP checksum algorithm begins in much the same way as the sum-of-bytes algorithm I discussed earlier. However, this algorithm is actually different. First, of course, we're computing a 16-bit checksum instead of an eight-bit one, so we're summing words rather than bytes. That difference is obvious. Less obvious is that we're actually computing a ones complement sum.
Recall that most computers store integers in a twos complement representation. Simply adding two integers, as we did in the previous algorithm, will therefore result in a twos complement sum. In order to compute the ones complement sum, we need to perform our addition with "end around carry." This means that carries out of the most significant bit (MSB) are not discarded, as they were previously. Instead, carries are added back into the checksum at the least significant bit (LSB). This could be done after each addition, but testing for a carry after each addition is expensive in C. A faster way is to let the carries accumulate in the upper half of a 32-bit accumulator. Once the sum-of-words is complete, the upper half of the 32-bit accumulator is turned into a 16-bit value and added to the 16-bit twos complement sum (the lower half). One final carry is possible at that point, and must be included in the final sum. The IP checksum is the inverted ones complement sum of all of the words in the IP header.
For checksum purposes, ones complement arithmetic has an important advantage over twos complement arithmetic. Recall that the biggest weakness of a parity bit is that it can't detect a pair of bit errors or any even number of errors, for that matter. A twos complement sum suffers from a similar weakness. Only one of the bits in the sum (the MSB) is affected by changes in the most significant of the 16 columns. If an even number of bit errors occurs within that column, the checksum will appear to be correct and the error will not be detected. A ones complement sum does not suffer this weakness.
Because carries out of the MSB are added back into the LSB during a ones complement sum, errors in any one column of the data will be reflected in more than one bit of the checksum. So a ones complement sum is a stronger checksum (for example, will detect more errors) than a twos complement sum, and only slightly more expensive. Hence, it is chosen for use in a lot of different situations.
The checksums within the UDP and TCP headers are computed in exactly the same way as the IP checksum. In fact, the only major difference is the set of words over which the sum is calculated. (A minor difference is that UDP checksums are optional.) In both cases, these layer 4 protocols include the message, their own header fields, and a few important fields of the IP header in the checksum calculation. The inclusion of some IP header fields in the UDP and TCP checksums is one of the biggest reasons that these layers of the protocol stack cannot be completely separated from the IP layer in a software implementation. The reason that IP checksums include only the IP header is that many intermediate computers must validate, read, and modify the contents of the IP header as a packet travels from its source to the destination. By reducing the number of words involved in the calculation, the speed with which all IP packets move across the Internet is improved. Including a larger set of words in the UDP and TCP checksums does not slow down communications; rather, it increases the likelihood that the message received is the same as the message sent.
Further reading
The checksum algorithms considered here are based on simple binary addition. That makes them relatively inexpensive to compute. However, these are weak checksum algorithms that will allow common types of hardware errors to escape detection.
A more sophisticated type of checksum is called a cyclic redundancy code (CRC). Related articles cover CRC mathematics and theory and CRC implementation in C.
This article began as a column in the November 1999 issue of Embedded Systems Programming.



