Checksum algorithms based solely on addition are easy to implement and can be executed efficiently on any microcontroller. However, many common types of transmission errors cannot be detected when such simple checksums are used. This article describes a stronger type of checksum, commonly known as a CRC.
A cyclic redundancy check (CRC) is based on division instead of addition. The error detection capabilities of a CRC make it a much stronger checksum and, therefore, often worth the price of additional computational complexity.
Download Barr Group's Free CRC Code in C now.
Additive checksums are error detection codes as opposed to error correction codes. A mismatch in the checksum will tell you there's been an error but not where or how to fix it. In implementation terms, there's not much difference between an error detection code and an error correction code. In both cases, you take the message you want to send, compute some mathematical function over its bits (usually called a checksum), and append the resulting bits to the message during transmission.
Error Correction
The difference between error detection and error correction lies primarily in what happens next. If the receiving system detects an error in the packet--for example, the received checksum bits do not accurately describe the received message bits--it may either discard the packet and request a retransmission (error detection) or attempt to repair the damage on its own (error correction). If packet repairs are to be attempted, the checksum is said to be an error correcting code.
The key to repairing corrupted packets is a stronger checksum algorithm. Specifically, what's needed is a checksum algorithm that distributes the set of valid bit sequences randomly and evenly across the entire set of possible bit sequences. For example, if the minimum number of bits that must change to turn any one valid packet into some other valid packet is seven, then any packet with three or fewer bit inversions can be corrected automatically by the receiver. (If four bit errors occur during transmission, the packet will seem closer to some other valid packet with only three errors in it.) In this case, error correction can only be done for up to three bit errors, while error detection can be done for up to six.
This spreading of the valid packets across the space of possible packets can be measured by the Hamming distance, which is the number of bit positions in which any two equal-length packets differ. In other words, it's the number of bit errors that must occur if one of those packets is to be incorrectly received as the other. A simple example is the case of the two binary strings 1001001 and 1011010, which are separated by a Hamming distance of three. (To see which bits must be changed, simply XOR the two strings together and note the bit positions that are set. In our example, the result is 0010011.)
The beauty of all this is that the mere presence of an error detection or correction code within a packet means that not all of the possible packets are valid. Figure 1 shows what a packet looks like after a checksum has been appended to it. Since the checksum bits contain redundant information (they are completely a function of the message bits that precede them), not all of the 2(m+c) possible packets are valid packets. In fact, the stronger the checksum algorithm used, the greater the number of invalid packets will be.

Figure 1. A packet of information including checksum
By adjusting the ratio of the lengths m and c and carefully selecting the checksum algorithm, we can increase the number of bits that must be in error for any one valid packet to be inadvertently changed into another valid packet during transmission or storage and, hence, the likelihood of successful transmission. In essence, what we want to do is to maximize the "minimum Hamming distance across the entire set of valid packets." In other words, to distribute the set of 2m valid packets as evenly as possible across the set of possible bit sequences of length m + c. This has the useful real-world effect of increasing the percentage of detectable and/or correctable errors.
Binary Long Division
It turns out that once you start to focus on maximizing the "minimum Hamming distance across the entire set of valid packets," it becomes obvious that simple checksum algorithms based on binary addition don't have the necessary properties. A change in one of the message bits does not affect enough of the checksum bits during addition. Fortunately, you don't have to develop a better checksum algorithm on your own. Researchers figured out long ago that modulo-2 binary division is the simplest mathematical operation that provides the necessary properties for a strong checksum.
All of the CRC formulas you will encounter are simply checksum algorithms based on modulo-2 binary division. Though some differences exist in the specifics across different CRC formulas, the basic mathematical process is always the same:
- The message bits are appended with c zero bits; this augmented message is the dividend
- A predetermined c+1-bit binary sequence, called the "generator polynomial", is the divisor
- The checksum is the c-bit remainder that results from the division operation
In other words, you divide the augmented message by the generator polynomial, discard the quotient, and use the remainder as your checksum. It turns out that the mathematically appealing aspect of division is that remainders fluctuate rapidly as small numbers of bits within the message are changed. Sums, products, and quotients do not share this property. To see what I mean, look at the example of modulo-2 division in Figure 2. In this example, the message contains eight bits while the checksum is to have four bits. As the division is performed, the remainder takes the values 0111, 1111, 0101, 1011, 1101, 0001, 0010, and, finally, 0100. The final remainder becomes the checksum for the given message.
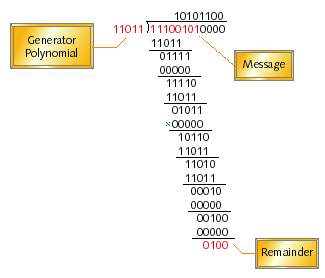
Figure 2. An example of modulo-2 binary division
For most people, the overwhelmingly confusing thing about CRCs is the implementation. Knowing that all CRC algorithms are simply long division algorithms in disguise doesn't help. Modulo-2 binary division doesn't map well to the instruction sets of general-purpose processors. So, whereas the implementation of a checksum algorithm based on addition is straightforward, the implementation of a binary division algorithm with an m+c-bit numerator and a c+1-bit denominator is nowhere close. [1] For one thing, there aren't generally any m+c or c+1-bit registers in which to store the operands. You will learn how to deal with this problem in the next article, where I talk about various software implementations of the CRC algorithms. For now, let's just focus on their strengths and weaknesses as potential checksums.
Generator Polynomials
Why is the predetermined c+1-bit divisor that's used to calculate a CRC called a generator polynomial? In my opinion, far too many explanations of CRCs actually try to answer that question. This leads their authors and readers down a long path that involves tons of detail about polynomial arithmetic and the mathematical basis for the usefulness of CRCs. This academic stuff is not important for understanding CRCs sufficiently to implement and/or use them and serves only to create potential confusion. So I'm not going to answer that question here. [2]
Suffice it to say here only that the divisor is sometimes called a generator polynomial and that you should never make up the divisor's value on your own. Several mathematically well-understood generator polynomials have been adopted as parts of various international communications standards; you should always use one of those. If you have a background in polynomial arithmetic then you know that certain generator polynomials are better than others for producing strong checksums. The ones that have been adopted internationally are among the best of these.
Table 1 lists some of the most commonly used generator polynomials for 16- and 32-bit CRCs. Remember that the width of the divisor is always one bit wider than the remainder. So, for example, you'd use a 17-bit generator polynomial whenever a 16-bit checksum is required.
|
|
Checksum Width
|
Generator Polynomial
|
|
CRC-CCITT
|
16 bits
|
10001000000100001
|
|
CRC-16
|
16 bits
|
11000000000000101
|
|
CRC-32
|
32 bits
|
100000100110000010001110110110111
|
Table 1. International standard CRC polynomials
As is the case with other types of checksums, the width of the CRC plays an important role in the error detection capabilities of the algorithm. Ignoring special types of errors that are always detected by a particular checksum algorithm, the percentage of detectable errors is limited strictly by the width of a checksum. A checksum of c bits can only take one of 2c unique values. Since the number of possible messages is significantly larger than that, the potential exists for two or more messages to have an identical checksum. If one of those messages is somehow transformed into one of the others during transmission, the checksum will appear correct and the receiver will unknowingly accept a bad message. The chance of this happening is directly related to the width of the checksum. Specifically, the chance of such an error is 1/2c. Therefore, the probability of any random error being detected is 1-1/2c.
To repeat, the probability of detecting any random error increases as the width of the checksum increases. Specifically, a 16-bit checksum will detect 99.9985% of all errors. This is far better than the 99.6094% detection rate of an eight-bit checksum, but not nearly as good as the 99.9999% detection rate of a 32-bit checksum. All of this applies to both CRCs and addition-based checksums. What really sets CRCs apart, however, is the number of special cases that can be detected 100% of the time. For example, I pointed out last month that two opposite bit inversions (one bit becoming 0, the other becoming 1) in the same column of an addition would cause the error to be undetected. Well, that's not the case with a CRC.
By using one of the mathematically well-understood generator polynomials like those in Table 1 to calculate a checksum, it's possible to state that the following types of errors will be detected without fail:
- A message with any one bit in error
- A message with any two bits in error (no matter how far apart, which column, and so on)
- A message with any odd number of bits in error (no matter where they are)
- A message with an error burst as wide as the checksum itself
The first class of detectable error is also detected by an addition-based checksum, or even a simple parity bit. However, the middle two classes of errors represent much stronger detection capabilities than those other types of checksum. The fourth class of detectable error sounds at first to be similar to a class of errors detected by addition-based checksums, but in the case of CRCs, any odd number of bit errors will be detected. So the set of error bursts too wide to detect is now limited to those with an even number of bit errors. All other types of errors fall into the relatively high 1-1/2c probability of detection.
Ethernet, SLIP, and PPP
Ethernet, like most physical layer protocols, employs a CRC rather than an additive checksum. Specifically, it employs the CRC-32 algorithm. The likelihood of an error in a packet sent over Ethernet being undetected is, therefore, extremely low. Many types of common transmission errors are detected 100% of the time, with the less likely ones detected 99.9999% of the time. Even if an error would somehow manage to get through at the Ethernet layer, it would probably be detected at the IP layer checksum (if the error is in the IP header) or in the TCP or UDP layer checksum above that. After all the chances of two or more different checksum algorithms not detecting the same error is extremely remote.
However, many embedded systems that use TCP/IP will not employ Ethernet. Instead, they will use either the serial line Internet protocol (SLIP) or point-to-point protocol (PPP) to send and receive IP packets directly over a serial connection of some sort. Unfortunately, SLIP does not add a checksum or a CRC to the data from the layers above. So unless a pair of modems with error correction capabilities sits in between the two communicating systems, any transmission errors must hope to be detected by the relatively weak, addition-based Internet checksum described last month. The newer, compressed SLIP (CSLIP) shares this weakness with its predecessor. PPP, on the other hand, does include a 16-bit CRC in each of its frames, which can carry the same maximum size IP packet as an Ethernet frame. So while PPP doesn't offer the same amount of error detection capability as Ethernet, by using PPP you'll at least avoid the much larger number of undetected errors that may occur with SLIP or CSLIP.
Read my article on CRC calculations in C, to learn about various software implementations of CRCs. We'll start with an inefficient, but comprehendible, implementation and work to gradually increase its efficiency. You'll see then that the desire for an efficient implementation is the cause of much of the confusion surrounding CRCs. In the meantime, stay connected..
Additional Resources
Download Barr Group's CRC Code-C (Free)
Related Barr Group Courses:
Embedded Linux Customization and Driver Development
For a full list of Barr Group courses, go to our Course Catalog.
Footnotes
[1] Implementing modulo-2 division is much more straightforward in hardware than it is in software. You simply need to shift the message bits through a linear feedback shift register as they are received. The bits of the divisor are represented by physical connections in the feedback paths. Due to the increased simplicity and efficiency, CRCs are usually implemented in hardware whenever possible.
[2] If you really want to understand the underlying mathematical basis for CRCs, I recommend the following reference: Bertsekas, Dimitri and Robert Gallager. Data Networks, second ed. Inglewood Cliffs, NJ: Prentice-Hall, 1992, pp. 61-64.
This article began as a column in the December 1999 issue of Embedded Systems Programming. If you wish to cite the article in your own work, you may find the following MLA-style information helpful:
Barr, Michael. "For the Love of the Game," Embedded Systems Programming, December 1999 , pp. 47-54.



