Finite impulse response (FIR) filters are the most popular type of filters implemented in software. This introduction will help you understand them both on a theoretical and a practical level.
Filters are signal conditioners. Each functions by accepting an input signal, blocking prespecified frequency components, and passing the original signal minus those components to the output. For example, a typical phone line acts as a filter that limits frequencies to a range considerably smaller than the range of frequencies human beings can hear. That's why listening to CD-quality music over the phone is not as pleasing to the ear as listening to it directly.
A digital filter takes a digital input, gives a digital output, and consists of digital components. In a typical digital filtering application, software running on a digital signal processor (DSP) reads input samples from an A/D converter, performs the mathematical manipulations dictated by theory for the required filter type, and outputs the result via a D/A converter.
An analog filter, by contrast, operates directly on the analog inputs and is built entirely with analog components, such as resistors, capacitors, and inductors.
Are you looking for an expert witness in digital signal processing?
There are many filter types, but the most common are lowpass, highpass, bandpass, and bandstop. A lowpass filter allows only low frequency signals (below some specified cutoff) through to its output, so it can be used to eliminate high frequencies. A lowpass filter is handy, in that regard, for limiting the uppermost range of frequencies in an audio signal; it's the type of filter that a phone line resembles.
A highpass filter does just the opposite, by rejecting only frequency components below some threshold. An example highpass application is cutting out the audible 60Hz AC power "hum", which can be picked up as noise accompanying almost any signal in the U.S.
The designer of a cell phone or any other sort of wireless transmitter would typically place an analog bandpass filter in its output RF stage, to ensure that only output signals within its narrow, government-authorized range of the frequency spectrum are transmitted.
Engineers can use bandstop filters, which pass both low and high frequencies, to block a predefined range of frequencies in the middle.
Frequency Response
Simple filters are usually defined by their responses to the individual frequency components that constitute the input signal. There are three different types of responses. A filter's response to different frequencies is characterized as passband, transition band, or stopband. The passband response is the filter's effect on frequency components that are passed through (mostly) unchanged.
Frequencies within a filter's stopband are, by contrast, highly attenuated. The transition band represents frequencies in the middle, which may receive some attenuation but are not removed completely from the output signal.
In Figure 1, which shows the frequency response of a lowpass filter, ωp is the passband ending frequency, ωs is the stopband beginning frequency, and As is the amount of attenuation in the stopband. Frequencies between ωp and ωs fall within the transition band and are attenuated to some lesser degree.
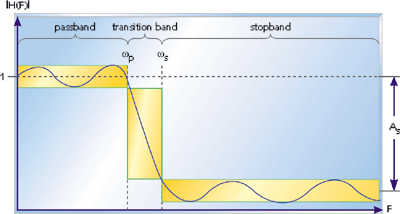
Figure 1. The response of a lowpass filter to various input frequencies
Given these individual filter parameters, one of numerous filter design software packages can generate the required signal processing equations and coefficients for implementation on a DSP. Before we can talk about specific implementations, however, some additional terms need to be introduced.
Ripple is usually specified as a peak-to-peak level in decibels. It describes how little or how much the filter's amplitude varies within a band. Smaller amounts of ripple represent more consistent response and are generally preferable.
Transition bandwidth describes how quickly a filter transitions from a passband to a stopband, or vice versa. The more rapid this transition, the higher the transition bandwidth; and the more difficult the filter is to achieve. Though an almost instantaneous transition to full attenuation is typically desired, real-world filters don't often have such ideal frequency response curves.
There is, however, a tradeoff between ripple and transition bandwidth, so that decreasing either will only serve to increase the other.
Finite Impulse Response
A finite impulse response (FIR) filter is a filter structure that can be used to implement almost any sort of frequency response digitally. An FIR filter is usually implemented by using a series of delays, multipliers, and adders to create the filter's output.
Figure 2 shows the basic block diagram for an FIR filter of length N. The delays result in operating on prior input samples. The hk values are the coefficients used for multiplication, so that the output at time n is the summation of all the delayed samples multiplied by the appropriate coefficients.
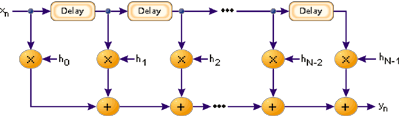
Figure 2. The logical structure of an FIR filter
The process of selecting the filter's length and coefficients is called filter design. The goal is to set those parameters such that certain desired stopband and passband parameters will result from running the filter. Most engineers utilize a program such as MATLAB to do their filter design. But whatever tool is used, the results of the design effort should be the same:
- A frequency response plot, like the one shown in Figure 1, which verifies that the filter meets the desired specifications, including ripple and transition bandwidth.
- The filter's length and coefficients.
The longer the filter (more taps), the more finely the response can be tuned.
With the length, N, and coefficients, float h[N] = { ... }, decided upon, the implementation of the FIR filter is fairly straightforward. Listing 1 shows how it could be done in C. Running this code on a processor with a multiply-and-accumulate instruction (and a compiler that knows how to use it) is essential to achieving a large number of taps.
/*
* Sample the input signal (perhaps via A/D).
*/
sample = input();
/*
* Insert the newest sample into an N-sample circular buffer.
* The oldest sample in the circular buffer is overwritten.
*/
x[oldest] = sample;
/*
* Multiply the last N inputs by the appropriate coefficients.
* Their sum is the current output.
*/
y = 0;
for (k = 0; k < N; k++)
{
y += h[k] * x[(oldest + k) % N];
}
oldest = (oldest + 1) % N;
/*
* Output the result.
*/
output(y);
Listing 1. Implementation of an N-tap FIR filter in C
As you can see, an FIR filter simply produces a weighted average of its N most recent input samples. All of the magic is in the coefficients, which dictate the actual output for a given pattern of input samples.
Other digital filter structures are possible, including infinite impulse response (IIR), which uses feedback to keep more historical information active in the calculation.
This article is dedicated to the memory of Brian Wagner. Prior to his death in 2002, Brian was an engineer at SenSyTech, where he developed software radio receiver systems. He earned a BSCE from Virginia Tech. This article was published posthumously.
This article was published in the December 2002 issue of Embedded Systems Programming. If you wish to cite the article in your own work, you may find the following MLA-style information helpful:
Wagner, Brian and Michael Barr. "Introduction to Digital Filters," Embedded Systems Programming, December 2002, pp. 47-48.



